Aplicaciones de las Máquinas de Vectores de Soporte

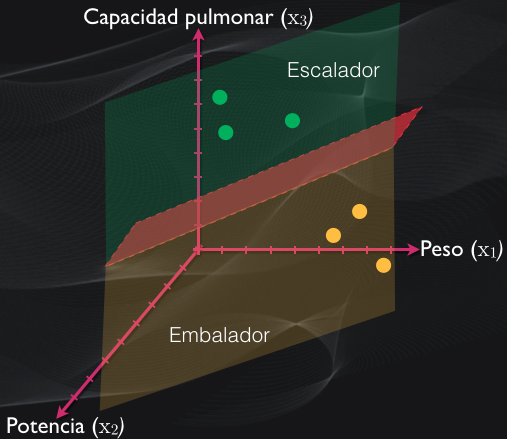
Las máquinas de vectores de soporte (SVM) son modelos de aprendizaje supervisado que se utilizan ampliamente en la clasificación y regresión de datos. Su objetivo principal es encontrar un hiperplano óptimo para separar las clases en un conjunto de datos. Esto significa que las SVM buscan la mejor manera de dividir los datos en diferentes grupos, maximizando la distancia entre el hiperplano y los puntos de datos más cercanos a él.

Uno de los componentes clave en las SVM son los vectores de soporte. Estos vectores son los puntos de datos que están más cerca del hiperplano, y juegan un papel crucial en la determinación y clasificación del mismo. Son estos vectores de soporte los que definen la posición y la orientación del hiperplano de separación, y permiten a las SVM realizar predicciones precisas en nuevos datos de prueba.

Las SVM son especialmente efectivas en el análisis de datos estructurados y en el reconocimiento de imágenes y patrones. Esto se debe a que las SVM pueden combinar diferentes características y extraer características importantes de los datos para realizar la clasificación. Por ejemplo, en el reconocimiento de imágenes, las SVM pueden identificar diferentes características visuales, como bordes, texturas o formas, y utilizarlas para clasificar las imágenes en diferentes categorías.

Una forma de mejorar aún más el rendimiento de las SVM en el reconocimiento de imágenes es mediante su combinación con redes neuronales convolucionales (CNN). Las CNN son un tipo de red neuronal que se basa en la idea de que las capas iniciales de una red deben identificar características simples, como bordes y formas geométricas, mientras que las capas posteriores deben combinar estas características para realizar clasificaciones más complejas. Al combinar SVM con CNN, se pueden aprovechar las fortalezas de ambos modelos y lograr resultados más precisos en la clasificación de imágenes.

Introducción

Las máquinas de vectores de soporte (SVM) son modelos de aprendizaje supervisado utilizados ampliamente en la clasificación y regresión de datos. Su objetivo principal es encontrar un hiperplano óptimo para separar las clases en un conjunto de datos. Esto implica buscar la mejor manera de dividir los datos en diferentes grupos, maximizando la distancia entre el hiperplano y los puntos de datos más cercanos a él.

Los vectores de soporte juegan un papel fundamental en las SVM, ya que son los puntos de datos que se encuentran más cerca del hiperplano de separación. Estos vectores determinan la posición y la orientación del hiperplano, lo que permite a las SVM realizar predicciones precisas en nuevos datos de prueba.

Las SVM son particularmente efectivas en el análisis de datos estructurados y en el reconocimiento de imágenes y patrones. Esto se debe a su capacidad para combinar diferentes características y extraer información relevante de los datos para la clasificación. Por ejemplo, en el reconocimiento de imágenes, las SVM pueden identificar características visuales, como bordes, texturas o formas, y utilizarlas para clasificar las imágenes en diferentes categorías.

Para mejorar aún más el rendimiento de las SVM en el reconocimiento de imágenes, se puede combinar esta técnica con redes neuronales convolucionales (CNN). Las CNN se basan en la idea de que las capas iniciales de una red deben identificar características simples, como bordes y formas geométricas, mientras que las capas posteriores combinan estas características para realizar clasificaciones más complejas. La combinación de SVM con CNN aprovecha las fortalezas de ambos modelos y puede lograr resultados más precisos en la clasificación de imágenes.

Características de las SVM

Las máquinas de vectores de soporte (SVM) tienen características distintivas que las hacen una técnica poderosa en el aprendizaje supervisado. Algunas de las características clave de las SVM son:

1. Hiperplanos y límites de decisión: Las SVM buscan encontrar un hiperplano óptimo que pueda separar de manera efectiva las clases en un conjunto de datos. El hiperplano es una superficie multidimensional que divide el espacio de características en dos partes, una para cada clase. Los límites de decisión son las regiones que definen la separación entre las clases.

2. Vectores de soporte: Los vectores de soporte son los puntos de datos más cercanos al hiperplano de separación. Estos puntos juegan un papel crucial en la determinación y clasificación del hiperplano. Las SVM se centran en estos puntos porque representan los datos más difíciles de clasificar y, por lo tanto, son fundamentales para lograr un modelo preciso.

3. Truco del núcleo: El truco del núcleo es una técnica que permite manejar datos no linealmente separables mediante la transformación de las características originales en un espacio de mayor dimensión. Esto permite la separación de las clases mediante un hiperplano en el espacio transformado, lo que hace posible la clasificación de datos que no se pueden dividir de manera lineal en el espacio de características original.

4. Aplicaciones en clasificación de datos: Las SVM se utilizan comúnmente en la clasificación de datos en dos o más clases. Pueden separar datos linealmente y también se pueden utilizar en la clasificación de datos no lineales. Además, las SVM son capaces de manejar conjuntos de datos desbalanceados, donde hay una desproporción significativa en el número de ejemplos de cada clase.

5. Aplicaciones en regresión: Además de la clasificación, las SVM también se pueden utilizar en problemas de regresión para predecir valores numéricos. La idea es utilizar un hiperplano que se ajuste a los datos de manera óptima y pueda predecir valores continuos en función de las características de entrada.

6. Aplicaciones en reconocimiento de imágenes y texto: Las SVM son particularmente efectivas en el reconocimiento y clasificación de imágenes y texto. Pueden identificar y extraer características relevantes de las imágenes, como bordes, texturas o formas, y utilizar estas características para clasificar las imágenes en diferentes categorías. En el caso del reconocimiento de texto, las SVM pueden analizar diferentes características, como las palabras utilizadas, la estructura del texto y las características sintácticas, para clasificar los documentos en diferentes categorías.

Las máquinas de vectores de soporte (SVM) son modelos de aprendizaje supervisado que ofrecen una amplia gama de aplicaciones en la clasificación de datos, la regresión y el reconocimiento de imágenes y texto. Su capacidad para encontrar hiperplanos óptimos, utilizar vectores de soporte y manejar datos no linealmente separables los convierte en una herramienta valiosa en el campo del aprendizaje automático.

Aplicaciones en reconocimiento de patrones

El reconocimiento de patrones es una aplicación clave de las máquinas de vectores de soporte (SVM). Estas técnicas son muy efectivas en el reconocimiento y clasificación de patrones en conjuntos de datos complejos. Algunas de las aplicaciones comunes de las SVM en el reconocimiento de patrones son las siguientes:

1. Reconocimiento de imágenes: Las SVM se utilizan ampliamente en el reconocimiento de objetos en imágenes. Estas técnicas pueden extraer características visuales de las imágenes, como bordes, texturas, colores, formas, utilizando una estructura jerárquica de clasificación. Esto permite reconocer objetos específicos y clasificar imágenes en diferentes categorías.

2. Reconocimiento de voz: Las SVM también se han aplicado exitosamente en el reconocimiento de voz. Se utilizan para clasificar y reconocer patrones en señales de voz, lo que permite la identificación de hablantes, la transcripción de voz a texto y otras aplicaciones de procesamiento de voz.

3. Filtrado de spam: Otro caso de aplicación de las SVM es en el filtrado de correos electrónicos no deseados o spam. Estas técnicas se utilizan para clasificar y distinguir entre correos electrónicos legítimos y correos no deseados, basándose en patrones y características específicas presentes en el contenido del correo electrónico.

4. Detección de anomalías: Las SVM también se utilizan en la detección de anomalías en conjuntos de datos. Se usan para identificar patrones que difieren significativamente de la mayoría de los ejemplos en el conjunto de datos, como en la detección de fraudes o en el monitoreo de sistemas industriales para la detección de fallas.

5. Reconocimiento de escritura a mano: Las SVM se aplican en el reconocimiento de caracteres y letras escritas a mano. Estas técnicas se utilizan en la identificación y clasificación de patrones escritos a mano, lo que permite el reconocimiento y transcripción de texto escrito a mano.

Las máquinas de vectores de soporte (SVM) tienen diversas aplicaciones en el reconocimiento de patrones, que incluyen el reconocimiento de imágenes, el reconocimiento de voz, el filtrado de spam, la detección de anomalías y el reconocimiento de escritura a mano. Estas aplicaciones se benefician de la capacidad de las SVM para aplicar vectores, extraer características y patrones relevantes de los datos y clasificarlos en diferentes categorías, lo que resulta en un reconocimiento preciso y una clasificación confiable.

Combinación con CNN

La combinación de las máquinas vector de soporte (SVM) con las redes neuronales convolucionales (CNN) es una estrategia poderosa para mejorar la precisión en el reconocimiento de imágenes.

Las redes neuronales convolucionales (CNN) son un tipo de red neuronal diseñada específicamente para procesar imágenes. Estas redes poseen capas convolucionales que extraen características visuales de las imágenes, como bordes, texturas y formas, y capas completamente conectadas que las utilizan para realizar la clasificación.

La combinación de las SVM con las CNN aprovecha las fortalezas de ambos modelos para lograr resultados aún más precisos en el reconocimiento de imágenes.

Primero, se utiliza la CNN para extraer características visuales de las imágenes y reducir la dimensionalidad de los datos. Estas características se convierten en vectores de entrada para las SVM. Luego, las SVM se entrenan utilizando estos vectores de características para clasificar las imágenes en diferentes categorías.

La razón detrás de esta combinación radica en que las SVM son muy efectivas en la clasificación de datos, pero pueden tener dificultades al tratar con grandes cantidades de datos o imágenes de alta dimensionalidad. Por otro lado, las CNN son expertas en el procesamiento de imágenes y la extracción de características, pero pueden tener dificultades para clasificar correctamente las imágenes.

Al combinar las SVM con las CNN, se utilizan las características de alta calidad extraídas por la CNN como entrada para las SVM, lo que permite una clasificación más precisa de las imágenes.

Esta combinación también permite aprovechar el rendimiento de las SVM en la clasificación multiclase y en el manejo de conjuntos de datos desbalanceados, ya que las SVM pueden manejar eficazmente variables categóricas y desigualdades en los datos.

La combinación de las máquinas vector de soporte (SVM) con las redes neuronales convolucionales (CNN) es una estrategia efectiva para mejorar la precisión en el reconocimiento de imágenes. Esta combinación permite aprovechar las fortalezas de ambos modelos y lograr resultados más precisos en la clasificación de imágenes en diferentes categorías.

Componentes clave de las SVM

Las máquinas de vectores de soporte (SVM) tienen varios componentes clave que juegan un papel fundamental en su funcionamiento. Estos componentes incluyen:

1. Hiperplanos y límites de decisión: Los hiperplanos son superficies multidimensionales que separan las clases en un conjunto de datos. En el caso de las SVM lineales, el hiperplano se define por una línea en un espacio bidimensional, mientras que en espacios de mayor dimensión, el hiperplano se convierte en un plano o una hipersuperficie. Los límites de decisión son las regiones que definen la separación entre las clases.

2. Vectores de soporte: Los vectores de soporte son los puntos de datos más cercanos al hiperplano de separación. Estos puntos juegan un papel crucial en la determinación y clasificación del hiperplano. Son estos vectores de soporte los que definen la posición y la orientación del hiperplano de separación, y permiten a las SVM realizar predicciones precisas en nuevos datos de prueba.

3. Truco del núcleo: El truco del núcleo es una técnica que permite manejar datos no linealmente separables mediante la transformación de las características originales en un espacio de mayor dimensión. En lugar de realizar la transformación explicita, el truco del núcleo utiliza una función de núcleo para realizar los cálculos necesarios. Esto permite a las SVM tratar los datos no lineales como si fueran lineales en el nuevo espacio de características, lo que facilita la clasificación.

4. Margen máximo: El margen máximo es la distancia perpendicular entre el hiperplano de separación y los vectores de soporte más cercanos. Las SVM buscan maximizar este margen, ya que un margen más amplio proporciona una clasificación más robusta y generalizable.

5. Costo de penalización: El costo de penalización es un parámetro ajustable en las SVM que controla la influencia de los errores de clasificación en la función objetivo del modelo. Un costo de penalización más alto penaliza más los errores de clasificación y puede conducir a un hiperplano más complejo y ajustado a los datos, mientras que un costo de penalización más bajo permite más errores de clasificación y puede resultar en un hiperplano más simple.

Los componentes clave de las máquinas de vectores de soporte (SVM) incluyen los hiperplanos y límites de decisión, los vectores de soporte, el truco del núcleo, el margen máximo y el costo de penalización. Estos componentes son fundamentales para el funcionamiento y el rendimiento de las SVM en la clasificación de los sistemas vectoriales y regresión de datos.

Diversas aplicaciones

Las máquinas de vectores de soporte (SVM) tienen múltiples aplicaciones en el campo del aprendizaje automático y la inteligencia artificial. Algunas de las aplicaciones más comunes de las SVM incluyen:

1. Clasificación de datos en dos o más clases: Las SVM son ampliamente utilizadas para la clasificación de datos en dos o más clases. Pueden separar datos linealmente y también se adaptan a la clasificación de datos no linealmente separables, utilizando técnicas como el truco del núcleo. Por ejemplo, pueden clasificar correos electrónicos como spam o no spam, o imágenes en diferentes categorías.

2. Regresión: Aunque las SVM son conocidas principalmente por su capacidad de clasificación, también se pueden aplicar en problemas de regresión. Las SVM pueden predecir valores numéricos a partir de datos de entrada, lo que las hace útiles en la estimación de variables continuas. Esto se logra ajustando un hiperplano a los datos que minimice el error de predicción.

3. Reconocimiento y clasificación de imágenes: Las SVM son ampliamente utilizadas en el reconocimiento y clasificación de imágenes debido a su capacidad para extraer características relevantes de las imágenes y realizar predicciones precisas. Pueden identificar patrones visuales, reconocer objetos, clasificar imágenes por contenido y ayudar en tareas de visión por computadora.

4. Análisis de texto y minería de datos: Las SVM se utilizan en el análisis de texto, donde ayudan a clasificar y categorizar documentos, como noticias, opiniones o comentarios. También se utilizan en la minería de datos para identificar patrones y tendencias en grandes conjuntos de datos de texto, como redes sociales, noticias o informes financieros.

5. Diagnóstico médico: Las SVM se aplican en el diagnóstico médico para ayudar a clasificar y predecir enfermedades. Pueden analizar datos médicos, como imágenes de resonancia magnética (MRI), resultados de pruebas de laboratorio o registros médicos, para ayudar en la detección y clasificación de enfermedades como cáncer, diabetes o enfermedades cardiovasculares.

6. Bioinformática: Las SVM se utilizan en la bioinformática para el análisis y clasificación de datos biológicos, como secuencias de ADN o proteínas. Pueden ayudar a identificar genes relacionados con enfermedades, predecir la estructura de proteínas o clasificar especies biológicas.

Estas son solo algunas de las muchas aplicaciones de las máquinas de vectores de soporte (SVM). Su flexibilidad, precisión y capacidad para manejar datos de alta dimensión las hacen una herramienta poderosa en una variedad de campos y disciplinas.